Lunar Terrain Generator

This project is a procedural lunar terrain heightmap generator for Python. The algorithm is grounded in established models of lunar geology and crater formation, generating realistic terrain at a scale of 1 meter per pixel.

To ensure realism, the generated terrain was validated against real lunar topographic statistics taken from the LROC RDR Data Portal. Note that the highest resolution data provided by the data portal is 2 meters per pixel, which motivated the creation of this generator to have access to data at 1 meter per pixel. The generator can produce distinct landscapes representative of the two key lunar types: smooth, basaltic Mare terrain and rugged, heavily-cratered Highland terrain.

Real vs. Generated Landscapes

A primary goal of this project was to generate synthetic terrain that is statistically and visually indistinguishable from real lunar topographies. Note that the terrains are created as 2d images (same as the LROC DTM data), and then later converted into meshes.

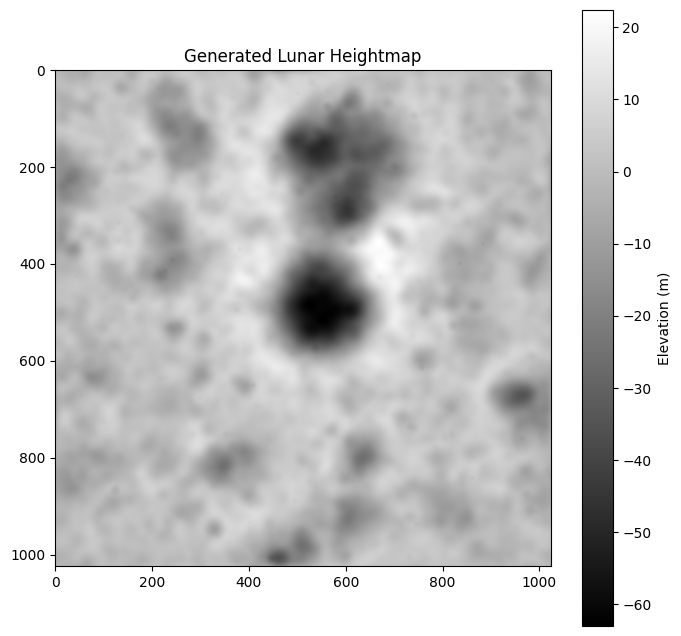
How it Works

The generator is implemented in Python and uses performance optimizations from Numba for parallel processing. The methodology is segmented into three primary stages:

1. Crater Profile Generation

First, a library of precomputed crater profiles is generated based on models derived from high-resolution LROC data. A crater’s morphology is a function of its diameter, $D$. The topographic profile is modeled by a piecewise function describing the flat central floor, the cubic polynomial of the inner wall, and the exponential decay of the exterior region.

1. Cratering Simulation

The algorithm simulates cratering events over a specified geological age. The number and size distribution of craters are determined using the Neukum production function and the lunar impact chronology curve. For each time step, crater diameters are sampled from this distribution and added to the heightmap at random locations, allowing the terrain to evolve over time.

1. Topographic Diffusion and Final Touches

Finally, the terrain undergoes a diffusion process to model the effects of long-term erosion and degradation. This is solved numerically by applying a finite-difference method based on the heat diffusion equation, which iteratively smooths sharp features. To enhance realism, the algorithm also adds high-frequency Perlin noise, simulates small rocks, and introduces small, young craters to complete the landscape.